Problemele de matematica ne pot da multora dintre noi batai de cap. Exista o multime de astfel de exercitii, aparent extrem de simple, care, in realitate nu au putu fi rezolvate nici macar de matematicieni. Va prezentam, in continuare, cateva exemple.
- Problema canapelei
Oricine s-a confruntat cu aceasta problema. Cand ne mutam dintr-un loc in altul si dorim sa luam si vechea canapea cu noi, exista mereu o problema cand trebuie sa o scoatem din camera, din cauza locurilor stramte si a colturilor prin care trebuie sa o strecuram. Privind problema in ansamblu, intr-o perspectiva bidimensonala, matematicienii doresc sa afle care este cea mai mare canapea care sa poata trece de un colt de 90 de grade, fara a fi indoita. Avery Thompson explica in publicatia Popular Mechanics: "Cel mai mare spatiu care se poate incadra in jurul unui colt se numeste - fara nicio gluma - 'constanta canapelei'. Aceasta constanta ar trebui sa se incadreze intre numerele 2.2195 si 2.8284, dar nimeni nu stie cu exactitate care poate fi cea mai mare canapea ce ar putea trece de un astfel de colt".
- Ipoteza numerelor prime gemene
Numerele prime sunt numerele divizibile doar cu ele insasi si cu 1. Din cate se stie, exista un numar infinit de numere prime si matematicienii incearca in mod constant sa gaseasca cel mai mare numar prim. Dar, exista si un numar infiit de perechi de numere prime diferite, cum sunt 41 sau 34, iar odata cu cresterea acestor numere, numerele prime gemene devin din ce in ce mai greu de regasit, desi, in teorie, ar trebui sa fie infinite. Problema este ca nimeni nu a putu dovedi acest lucru pana acum.
- Ipoteza Goldbach
O alta intrebare, aparent simpla, ii pune pe matematicieni in dificultate: este orice numar mai mare decat 2 egal cu suma a doua numere prime?
Desi am fi tentati sa raspundem afirmativ, deoarece exista exemple clare si simple in acest snens (1 +2 = 3; 3 + 1 = 4 etc.), odata cu inceperea efectuarii calculelor cu numere foarte mari, vor aparea mereu rezultate care sa se abata de la aceasta ipoteza. Asadar, inca nu s-a gasit un raspuns concret pentru aceasta intrebare.
- Ipoteza Beal
A, B, C, x, y si z sunt numere intregi pozitive (mai mari ca 0). Daca Ax + By = Cz , atunci A, B si C ar trebui sa aiba factor comun un numar prim (adica A, B si C sa fie divizibile cu acelasi numar prim). Sa zicem ca A = 15, B = 10 si C = 5. Toate acestea care au in comun factorul prim 5. Problema este ca daca x, y si z ar avea o valoare mai mare de 2, intreaga ipoteza este contrazisa.
Exemplu: 51 + 101 = 151
dar 52 + 102 ≠ 152
- Ipoteza patratului in bucla
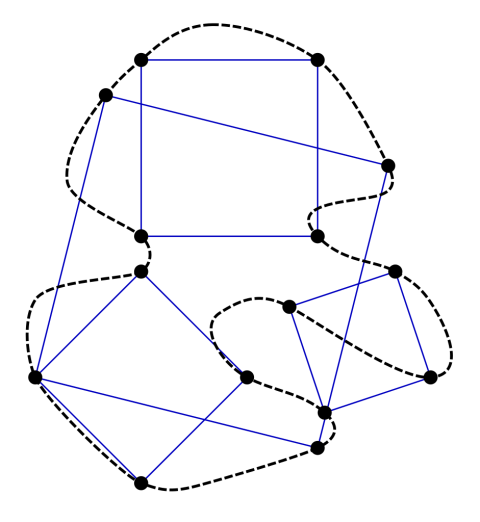
Desenati pe o coala de hartie o forma geometrica neregulata, o bucla, precum este in diagrama de sus. Conform acestei ipoteze, ar trebui sa putem desena in interiorul buclei un patrat care sa aiba toate colturile pe linia buclei. Matematic vorbind, exista o multitudine de forme de bucle si inca nu s-a putut dovedi ca aceasta ipoteza este valabila in toate cazurile. Alte forme geometrice precum triunghiurile sau paralelipipedele nu se abat de la aceasta regula, dar cand vine vorba de patrate, lucrurile devin mai complicate.
- Ipoteza Collatz
Desi aceasta ipoteza poate fi explicata si unui elev de scoala primara, ea ramane una dintre renumitele probleme de matematica ce nu si-au gasit, inca, rezolvarea. Ipoteza Collaz suna astfel: alege un numar, orice numar. Daca este un numar impar, inmulteste-l cu 3 si aduna-l cu 1. Daca este par, imparte-l la 2. Repeta aceasta operatiune cu noul numar obtinut si vei vedea ca, de fiecare data, vei ajunge la 1. Matematicienii au demonstrat ca exista milioane de numere in cazul carora aceasta ipoteza chiar functioneaza, dar problema este ca nu s-au putut gasi numere care sa contrazica aceasta regula. Cu toate acestea, "ar putea exista vreun numar mare care sa duca spre infinit sau unul care sa ramana blocat intr-o bucla si sa nu ajunga niciodata la 1", spune Thompson.